Sliding Window Technique is a method used to solve problems that involve subarray or substring or window. The basic idea behind the sliding window technique is to transform two nested loops into a single loop.
This method drastically reduces time complexity, often from O(n²) to O(n), making it indispensable for coding interviews and real-world optimizations.
What is the Sliding Window Technique?
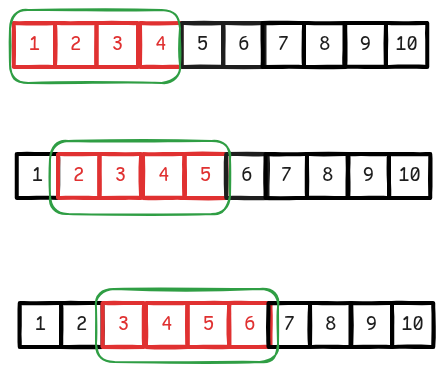
Let’s consider the array: [1,2,3,4,5,6,7,8,9,10] and a window size of 4.
- You start at index: 0 with window of 4 elements: [1,2,3,4]
- Than you move to next index 1 with window of 4 elements: [2,3,4,5]
- You added element on right
- You removed element from the left
- You kept the window of 4 as fixed size
- So on until you reach to the end of the array.....
Types of Sliding Windows:
- Fixed-Size Window – The window size remains constant
Problem: Maximum Sum of k Consecutive Elements
function maxSumSubarray(arr: number[], k: number): number {
let maxSum = 0;
let windowSum = 0;
// Calculate initial window sum
for (let i = 0; i < k; i++) {
windowSum += arr[i];
}
maxSum = windowSum;
// Slide the window
for (let i = k; i < arr.length; i++) {
// Subtract left, add right
windowSum = windowSum - arr[i - k] + arr[i];
maxSum = Math.max(maxSum, windowSum);
}
return maxSum;
}
// Example:
const arr = [1, 4, 2, 10, 2, 3, 1, 0];
console.log(maxSumSubarray(arr, 3)); // Output: 16 (from [4, 2, 10])- Variable-Size Window – The window expands or shrinks based on conditions
Problem: Longest Substring Without Repeating Characters
function longestUniqueSubstring(s: string): number {
let start = 0;
let maxLength = 0;
const charMap = new Map();
for (let end = 0; end < s.length; end++) {
const currentChar = s[end];
// If character exists in map, move start ahead
if (charMap.has(currentChar)) {
start = Math.max(start, charMap.get(currentChar)! + 1);
}
charMap.set(currentChar, end); // Update last seen index
maxLength = Math.max(maxLength, end - start + 1);
}
return maxLength;
}
// Example:
console.log(longestUniqueSubstring("abcabcbb")); // Output: 3 ("abc") Real-World Analogy: The Moving Train
Imagine a train moving along a track with N compartments. You want to find the maximum number of passengers in any three consecutive compartments.
- Brute Force Approach: Check every possible trio of compartments, leading to O(N²) time.
- Sliding Window Approach: Instead of recalculating, subtract the leaving compartment and add the entering one, resulting in O(N) time.
This is the essence of the sliding window—efficiently reusing computations instead of recalculating from scratch.
Why Sliding Window Beats Brute Force?
| Approach | Time Complexity | Space Complexity |
|---|---|---|
| Brute Force | O(n²) | O(1) |
| Sliding Window | O(n) | O(1) or O(k) |
By avoiding nested loops, the sliding window technique optimizes performance, making it ideal for large datasets.
When to Use the Sliding Window Technique?
This technique shines in problems with:
✔ Sequential data (arrays, strings, linked lists)
✔ Contiguous subarray/substring requirements
✔ Optimization goals (e.g., max/min sum, longest/shortest sequence)