Array Sorting Techniques

Sorting is a fundamental operation in programming that organizes data in a specific order (ascending, descending, or custom).

You can classify sorting algorithms as below:

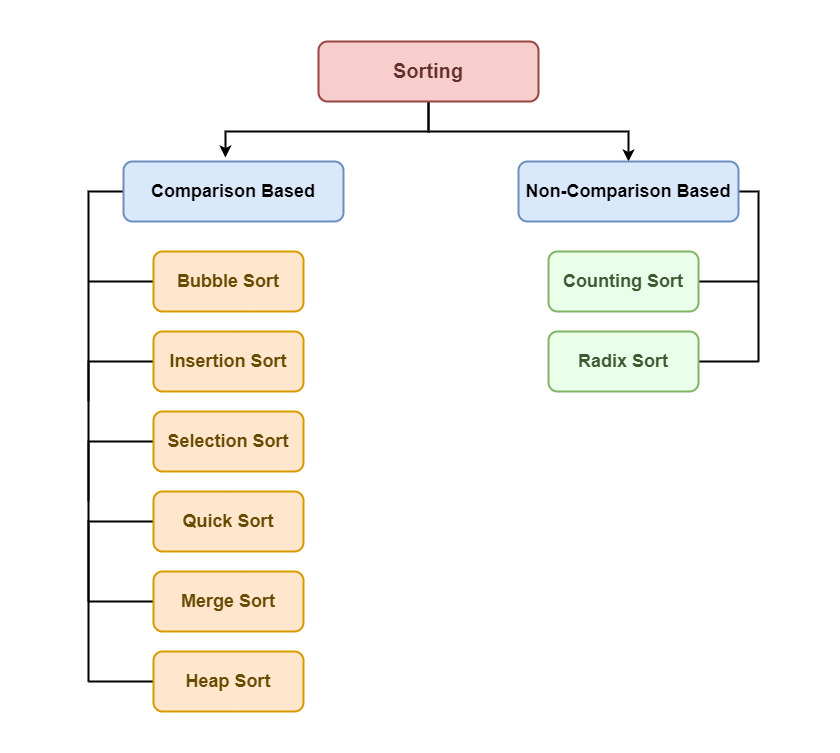
Efficient sorting improves search performance, enhances readability, and optimizes other algorithms. In this guide, we'll explore various sorting techniques, their time complexities, and when to use them—with TypeScript examples for clarity.

1. Bubble Sort

Bubble sort repeatedly swaps adjacent elements if they are in the wrong order.

• When to use: Small datasets or educational purposes (not efficient for large data).
• Time Complexity:
• Best Case: O(n) (already sorted)
• Average/Worst Case: O(n²)

Problem: Sorting array in ascending or descending order.

function bubbleSort(arr: number[]): number[] {
  const len = arr.length;

  for (let i = 0; i < len; i++) {
    for (let j = 0; j < n - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }

  return arr;
}

Video Explanation: Bubble Sort Explained

2. Selection Sort

Selection sort divides the array into a sorted and unsorted part, repeatedly selecting the smallest element from the unsorted portion.

• When to use: Small datasets where memory writes are costly (minimal swaps).
• Time Complexity:
• Best/Average/Worst Case: O(n²)

Problem: Sorting array in ascending or descending order.

function selectionSort(arr: number[]): number[] {
  const len = arr.length;

  for (let i = 0; i < len; i++) {
    let smallest = i;

    for (let j = i + 1; j < len; j++) {
      if (arr[smallest] > arr[j]) {
        smallest = i;
      }
    }

    [arr[i], arr[smallest]] = [arr[smallest], arr[i]];
  }

  return arr;
}

Video Explanation: Selection Sort Explained

3. Insertion Sort

Insertion sort builds the sorted array one element at a time by inserting each element into its correct position.

• When to use: Small or nearly sorted datasets.
• Time Complexity:
• Best Case: O(n) (already sorted)
• Average/Worst Case: O(n²)

Problem: Sorting array in ascending or descending order.

function insertionSort(arr: number[]): void {
  const len = arr.length;

  for (let i = 1; i < len; i++) {
    const currentPosition = arr[i];

    let prevPosition = i - 1;

    while (arr >= 0 && arr[prevPosition] > currentPosition) {
      arr[prevPosition + 1] = arr[prevPosition]; // Shift right
      prevPosition--;
    }

    arr[prevPosition + 1] = currentPosition;
  }
}

Video Explanation: Insertion Sort Explained

4. Merge Sort (Divide & Conquer)

Merge sort recursively splits the array into halves, sorts them, and merges them back.

• When to use: Large datasets, stable sorting required.
• Time Complexity:
• Best/Average/Worst Case: O(n log n)

Problem: Sorting array in ascending or descending order.

function mergeSort(arr: number[]): number[] {
  // base case: for single or empty array
  if (arr.length <= 1) return arr;

  // divide: divide array
  const midIndex = Math.floor(arr.length / 2);

  // conquer: solve left/right part of the array
  const leftArr = mergeSort(arr.slice(0, midIndex)); // O(log n)
  const rightArr = mergeSort(arr.slice(midIndex));

  // combine: combine the solution
  return merge(leftArr, rightArr); // O(n)
}

function merge(leftArr: number[], rightArr: number[]): number[] {
  let i = 0;
  let j = 0;
  let result: number[] = [];

  while (i < leftArr.length && j < rightArr.length) {
    if (leftArr[i] < rightArr[j]) {
      result.push(leftArr[i]);
      i++;
    } else {
      result.push(rightArr[j]);
      j++;
    }
  }

  return result.concat(leftArr.slice(i)).concat(rightArr.slice(j));
}

Video Explanation: Merge Sort Explained

5. Quick Sort (Divide & Conquer)

Quick sort picks a "pivot," partitions the array around it, and recursively sorts subarrays.

• When to use: Large datasets, average-case efficiency matters.
• Time Complexity:
• Best/Average Case: O(n log n)
• Worst Case: O(n²) (when pivot is poorly chosen)

Problem: Sorting array in ascending or descending order.

function quickSort(arr: number[]): number[] {
    if (arr.length <= 1) return arr;

    const pivot = arr[Math.floor(arr.length / 2)];
    const left = arr.filter(x => x < pivot);
    const middle = arr.filter(x => x === pivot);
    const right = arr.filter(x => x > pivot);

    return [...quickSort(left), ...middle, ...quickSort(right)];
}

Video Explanation: Quick Sort Explained

6. Heap Sort

Heap sort converts the array into a max-heap and repeatedly extracts the largest element.

• When to use: In-place sorting with O(n log n) worst-case guarantee.
• Time Complexity:
• Best/Average/Worst Case: O(n log n)

Problem: Sorting array in ascending or descending order.

function heapSort(arr: number[]): number[] {
    const n = arr.length;

    // Build max heap
    for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
        heapify(arr, n, i);
    }

    // Extract elements one by one
    for (let i = n - 1; i > 0; i--) {
        [arr[0], arr[i]] = [arr[i], arr[0]]; // Swap root with last element
        heapify(arr, i, 0); // Heapify reduced heap
    }
    return arr;
}

function heapify(arr: number[], n: number, i: number): void {
    let largest = i;
    const left = 2 * i + 1;
    const right = 2 * i + 2;

    if (left < n && arr[left] > arr[largest]) largest = left;
    if (right < n && arr[right] > arr[largest]) largest = right;

    if (largest !== i) {
        [arr[i], arr[largest]] = [arr[largest], arr[i]];
        heapify(arr, n, largest);
    }
}

When to Use Which Sorting Algorithm?

• Small datasets? → Insertion Sort (simple, fast for nearly sorted data).
• Large datasets? → Merge Sort (stable, consistent O(n log n)).
• Average-case efficiency? → Quick Sort (fastest in practice).
• Memory constraints? → Heap Sort (in-place, O(1) space).
• Learning purposes? → Bubble/Selection Sort (easy to understand).